In quest’articolo scoprirai cos’è la curvatura in un punto della deformata di una trave o di un pilastro, qual è la formula analitica approssimata e quella rigorosa per il calcolo di tale parametro e perché è così importante l’ipotesi di piccoli spostamenti che si adotta nell’analisi strutturale.

Nel corso dell’articolo potrai scaricare gratuitamente una risorsa utility, implementata in Microsoft Excel, che ti consentirà di comprendere il concetto di curvatura grazie ad una simulazione interattiva. Potrai spostare un punto su tre tipi di curve ed osservare come varia il cerchio osculatore ed il valore della curvatura nel punto selezionato. Potrai selezionare la formula approssimata o quella rigorosa per valutare le differenze in termini di risultati.
Potrai scaricare la nuova risorsa nel corso dell’articolo dell’articolo. Buona lettura!
Scarica la risorsa utility sulla curvatura

Scarica la risorsa implementata in Microsoft Excel per la simulazione interattiva sul calcolo della curvatura in un punto della deformata di una trave. Compila i campi qui sotto. Riceverai all’istante il link per eseguire il download.

Curvatura della deformata in un punto: perché è importante per la progettazione strutturale
La curvatura calcolata in un punto della configurazione deformata di una trave o di un pilastro è un parametro oggetto di verifica ai sensi delle NTC2018 e Circolare 2019. La Normativa Tecnica prescrive di eseguire una verifica sulla duttilità di curvatura degli elementi strutturali in calcestruzzo armato (trovi un approfondimento sul tema a questo link). Pertanto per comprendere appieno la verifica sulla duttilità di curvatura è fondamentale avere ben chiaro cos’è la curvatura in un punto della deformata di una trave e come si calcola.
Per questo motivo ho creato una risorsa utility che ti consentirà di eseguire delle simulazioni interattive sul concetto di curvatura. Nel seguito dell’articolo ti mostro come funziona tale risorsa e come puoi utilizzarla al meglio. Scoprirai anche qual è la formula analitica per il calcolo della curvatura, nella forma completa e approssimata.
Risorsa utility sulla curvatura: scegli una fra le tre curve disponibili
Dopo aver attivato le macro all’avvio dell’applicazione, nella schermata principale troverai tre pulsanti che ti permetteranno di selezionare una fra tre diverse curve. Si tratta di curve polinomiali di terzo grado del tipo y(x) = a∙x3+b∙x2+c∙x+d ottenute facendo variare il valore dei coefficienti a, b, c, d del polinomio come indicato di seguito:
- curva 1: a=0, b=0.10, c=0 d=0
- curva 2: a=-0.01, b=0, c=1 d=4
- curva 3: a=-0.10, b=0, c=1 d=4
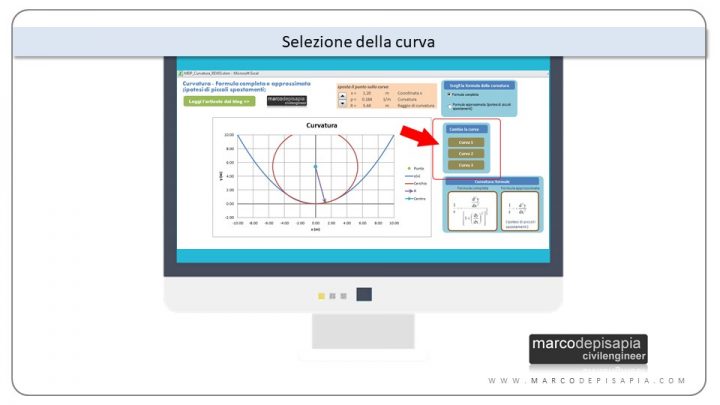
Dopo aver selezionato una curva, potrai visualizzarla nel piano cartesiano x,y. Puoi immaginare queste curve come la deformata dell’asse di una trave. C’è però una precisazione da fare. L’ipotesi di piccoli spostamenti in tal caso non è rispettata.
Se ci fai caso infatti la massima ordinata che puoi vedere nel grafico (la puoi immaginare come lo spostamento verticale dell’asse di una trave) è dello stesso ordine di grandezza dell’ascissa massima.
Ti ricordo che per rispettare l’ipotesi di piccoli spostamenti, lo spostamento massimo in mezzeria di una trave appoggiata-appoggiata, per esempio, dovrà essere minore di circa un trentesimo della luce (te ne ho parlato in quest’articolo). In questo caso la relazione precedente non è rispettata.
Risorsa utility: sposta il punto sulla curva
Nella parte alta dell’applicazione troverai due pulsanti freccia che puoi utilizzare per spostare il punto di interesse sulla curva. Per ogni posizione del punto, potrai vedere il raggio di curvatura in quel punto e il cerchio osculatore corrispondente. La curvatura di una curva in un punto si calcola come l’inverso del raggio del cerchio osculatore:
Curvatura: ρ = 1/R
- ρ curvatura;
- R raggio del cerchio osculatore.

Formula analitica completa o approssimata per il calcolo della curvatura
C’è poi un altro comando molto utile al nostro scopo. Si tratta di una finestra di selezione che ti permette di scegliere la formula da utilizzare per calcolare la curvatura della curva nel punto selezionato. Puoi scegliere fra due opzioni:
- formula completa
- formula approssimata
Se scegli l’opzione formula completa verrà calcolata la curvatura esatta nel punto della curva selezionato. La formula utilizzata è la seguente:
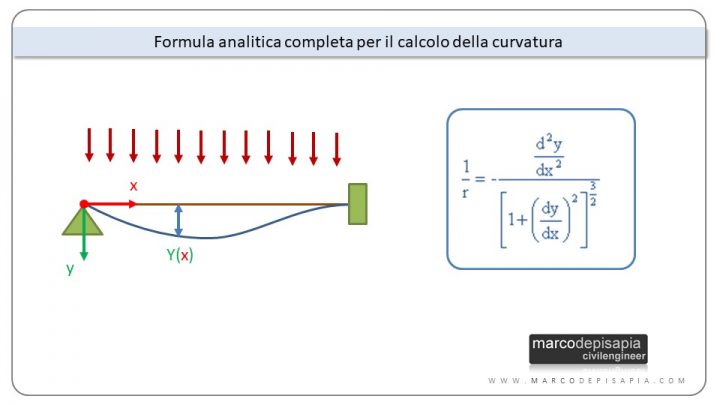
Nel caso di validità dell’ipotesi di piccoli spostamenti, il valore della derivata prima della funzione y(x) elevato al quadrato al denominatore può essere trascurato, perché sarebbe un infinitesimo di ordine superiore. Pertanto l’espressione della curvatura si semplifica e coinciderà con la derivata seconda della funzione y(x). Puoi vedere la formula qui di seguito:
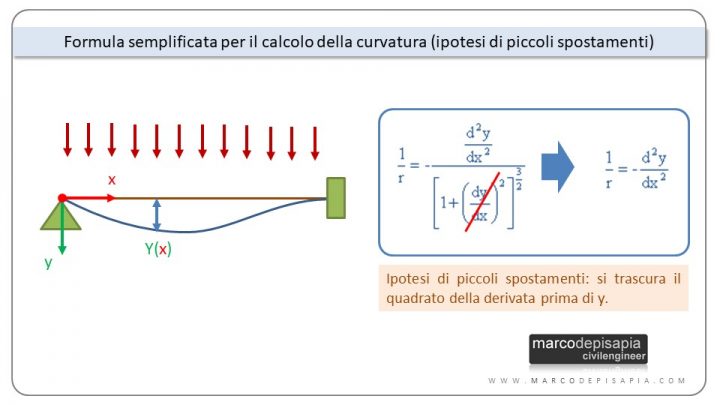
Quando l’ipotesi di piccoli spostamenti non è rispettata, la formula semplificata della curvatura darà come risultato un valore sensibilmente diverso da quello calcolato con la formula completa, nel caso in cui posizioni il cursore in un punto della curva con valore della derivata prima elevato. Puoi vedere qui in basso l’esempio del confronto fra la curvatura calcolata con la formula completa e quella calcolata con la formula approssimata nel punto della curva indicato in figura.
- curvatura nel punto selezionato calcolata con la formula completa: 1/R = 0.170 [1/m]
- curvatura nel punto selezionato calcolata con la formula semplificata: 1/R = 0.492 [1/m]
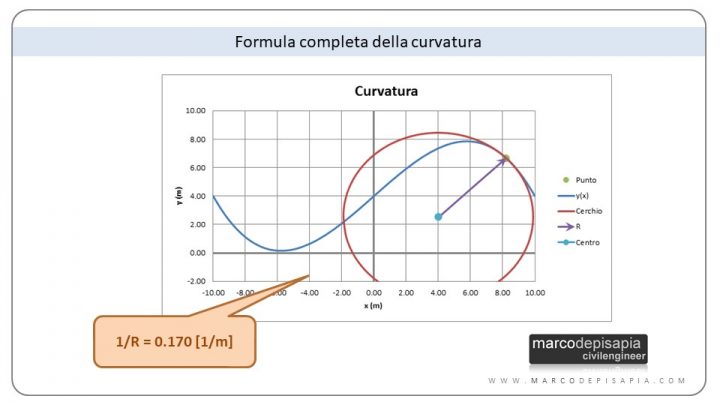
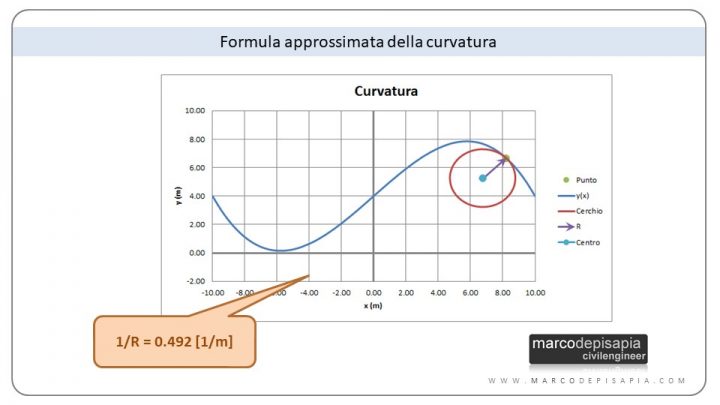
I valori delle curvature ottenute con le due formule tenderanno a coincidere se posizioni il punto in zone della curva in cui il valore della derivata prima è molto piccolo, ovvero quelle zone della curva in cui la tangente alla curva in quel punto è quasi orizzontale.
In questi punti il valore della curvatura ottenuto con le due diverse formulazioni è quasi coincidente. Puoi provarlo tu stesso passando da una formulazione all’altra e leggendo il valore numerico del raggio di curvatura nella parte alta del foglio. Vedrai che il valore del raggio sarà variato di pochissimo.
Nella Teoria Tecnica della Trave vale l’ipotesi di piccoli spostamenti, in quanto le strutture presentano valori di spostamenti e deformazioni molto ridotti rispetto alle dimensioni degli elementi strutturali, pertanto risulterà lecito approssimare l’espressione della curvatura con la sua forma semplificata in modo da rendere più agevole il calcolo.
Scarica la risorsa utility sulla curvatura

E’ arrivato il momento di provare la risorsa interattiva sulla curvatura. Per eseguire il download compila i campi qui sotto. Riceverai all’istante un’email contenente il link per scaricare la risorsa.

Conclusioni
Probabilmente questo post sarà apprezzato in particolar modo dai lettori che stanno completando il loro percorso di studi universitari. Se sei un professionista forse lo troverai poco pratico per il tuo lavoro. Ad ogni modo, richiamare alla memoria concetti chiave per l’analisi strutturale sicuramente ti aiuterà ad eseguire un calcolo strutturale con maggiore sicurezza, evitando di commettere errori grossolani.
Ad esempio, se nel tuo software di calcolo applichi al modello carichi eccessivamente grandi, otterrai spostamenti altrettanto grandi, magari ben oltre il limite consentito per la validità dell’ipotesi di piccoli spostamenti. In tal caso i risultati ottenuti dal tuo software di calcolo in termini di spostamenti e sollecitazioni non saranno più validi.
L’espressione semplificata della curvatura, definita tramite la derivata prima della funzione spostamento, è utilizzata per esprimere il legame momento-curvatura della sezione retta ai fini della risoluzione del problema della linea elastica per una trave comunque caricata e vincolata. La validità della formula approssimata per il calcolo della curvatura è garantita solo nell’ipotesi di piccoli spostamenti.
Mi auguro che questo post e la risorsa allegata ti abbiano aiutato a comprendere pienamente la formula analitica per il calcolo della curvatura e i casi in cui può essere utilizzata la sua versione approssimata. Se quest’articolo ti è piaciuto, puoi suggerirlo ai tuoi colleghi su Linkedin o ai tuoi amici su Facebook cliccando sui tasti di condivisione social che trovi in fondo alla pagina.
Al prossimo post.
Marco
Ultimo aggiornamento: 11/2/2023. Pubblicato il 27/3/2017. Codice articolo: 218
