Fondazione su suolo elastico alla Winkler o incastri alla base? Se questo dubbio ti assale durante le fasi di creazione del modello di calcolo per l’analisi strutturale di una costruzione, allora sono certo che quest’articolo potrà esserti d’aiuto.
In questo post scoprirai quando è possibile modellare la trave di fondazione su suolo elastico alla Winkler e quando invece dovrai applicare obbligatoriamente degli incastri alla base, secondo le prescrizioni delle NTC2018.

Nel corso dell’articolo vedremo inoltre:
- quale ipotesi scegliere fra fondazione rigida o deformabile in fase di progetto;
- l’influenza del valore della costante di sottofondo (k di Winkler) sulle sollecitazioni della trave di fondazione;
- cosa accade quando il k di Winkler varia in direzione orizzontale.
Buona lettura.
Scarica l’app Plate Design (xls di Microsoft Excel) per la verifica strutturale e geotecnica di fondazioni a platea

Plate Design è l’app per il progetto e verifica di fondazioni a platea in calcestruzzo armato implementata in Microsoft Excel. Puoi scaricare la versione gratuita dell’app compilando i campi qui sotto. Riceverai all’istante una mail contenente il link per eseguire il download.

La scelta fra suolo alla Winkler e incastri alla base: il limite del 70% prescritto dalle NTC2018
In fase di modellazione della struttura oggetto di analisi potrai scegliere fra due soluzioni alternative per le fondazioni:
- modellare la sovrastruttura con base fissa, assegnando dei vincoli di incastro alla base dei pilastri; dovrai poi calcolare separatamente la sola fondazione su suolo elastico, assegnando come carichi le reazioni vincolari della sovrastruttura incastrata alla base;
- creare un unico modello che comprenda la sovrastruttura e la fondazione su suolo elastico alla Winkler.
Le NTC2018 impongono il rispetto di una condizione nel caso si scelga la soluzione 2. Ti riporto di seguito l’estratto della Normativa Tecnica:
Ove si effettuino analisi di interazione terreno-struttura, la risultante globale di taglio e sforzo normale trasmessa all’estradosso della fondazione della costruzione deve essere almeno pari al 70% di quella ottenuta da identico modello strutturale con vincoli fissi all’estradosso della fondazione e con input sismico corrispondente allo spettro di risposta per sottosuolo tipo A.
par. 7.2.6 – NTC2018
In sostanza se decidi di modellare la fondazione su suolo alla Winkler, dovrai creare un secondo modello di calcolo, identico al primo, ma con incastri alla base, dando in input uno spettro di risposta per sottosuolo A. Potrai utilizzare i risultati del modello con fondazione su suolo alla Winkler se il tagliante alla base e il carico verticale risultante saranno almeno pari al 70% dei valori ottenuti dal modello con incastri alla base.
Il modello di suolo alla Winkler e la rigidezza relativa fondazione/terreno
Il modello più utilizzato per il calcolo delle sollecitazioni negli elementi di fondazione è il modello di suolo alla Winkler. Il terreno di fondazione viene schematizzato come un letto di molle di rigidezza k (noto anche come k di Winkler) indipendenti fra loro. Di conseguenza l’abbassamento di una molla non influenza l’abbassamento della molla adiacente.
Esistono diversi metodi per stimare il valore del k di Winkler, li trovi elencati in quest’articolo. Una volta nota la rigidezza k del terreno, il passo successivo consiste nel dimensionamento della sezione della trave di fondazione.
La sezione della trave di fondazione dovrà avere un’adeguata rigidezza flessionale. A tal proposito voglio mostrarti i due casi limite seguenti:
- trave di fondazione infinitamente flessibile rispetto alla rigidezza del terreno;
- trave di fondazione infinitamente rigida rispetto alla rigidezza del terreno.
Per mostrarti la differenza fra questi due casi limite, ho utilizzato dei modelli creati in Ca.Tel.2D, l’app del blog per la risoluzione di schemi strutturali piani (in Ca.Tel.2D puoi modellare anche travi di fondazione su suolo elastico come mostrato in questo tutorial).
Il modello creato riproduce un telaio a due livelli e due campate con trave di fondazione su suolo alla Winkler, composto dai seguenti elementi strutturali:
- travi di sezioni 30×50;
- pilastri di sezione 30×70;
- k di Winkler = 3 kg/cm^3;
- altezze di piano = 3 m;
- luce delle campate: 5 m e 4 m.
Primo schema limite: trave con modesta rigidezza flessionale
Il primo caso riguarda il caso di fondazione con bassa rigidezza flessionale. Per riprodurlo ho assegnato alla trave di fondazione una sezione di altezza ridotta, appena 10 cm per una base di 100 cm. Ecco il risultato in termini di deformata e sollecitazioni flettenti.
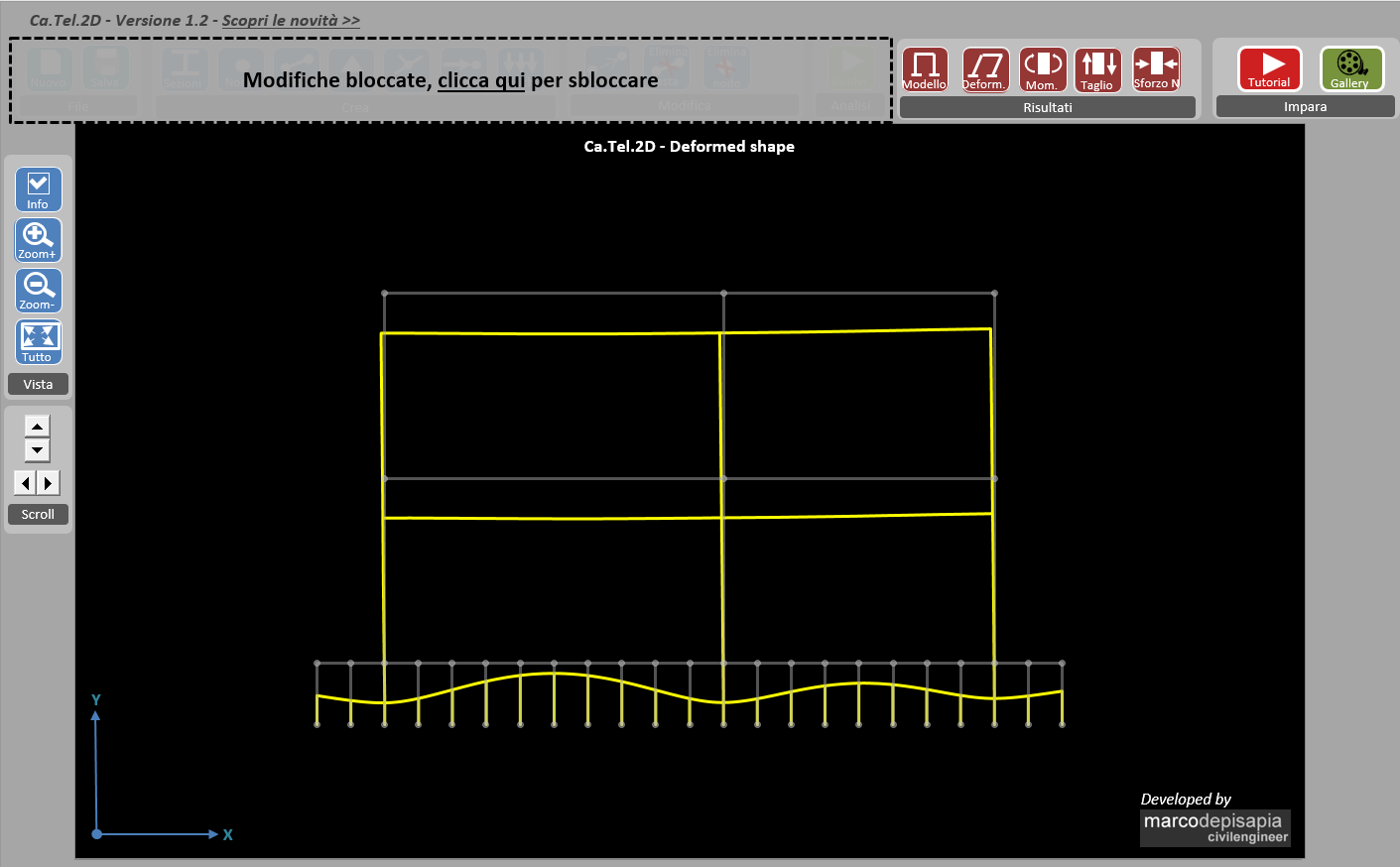
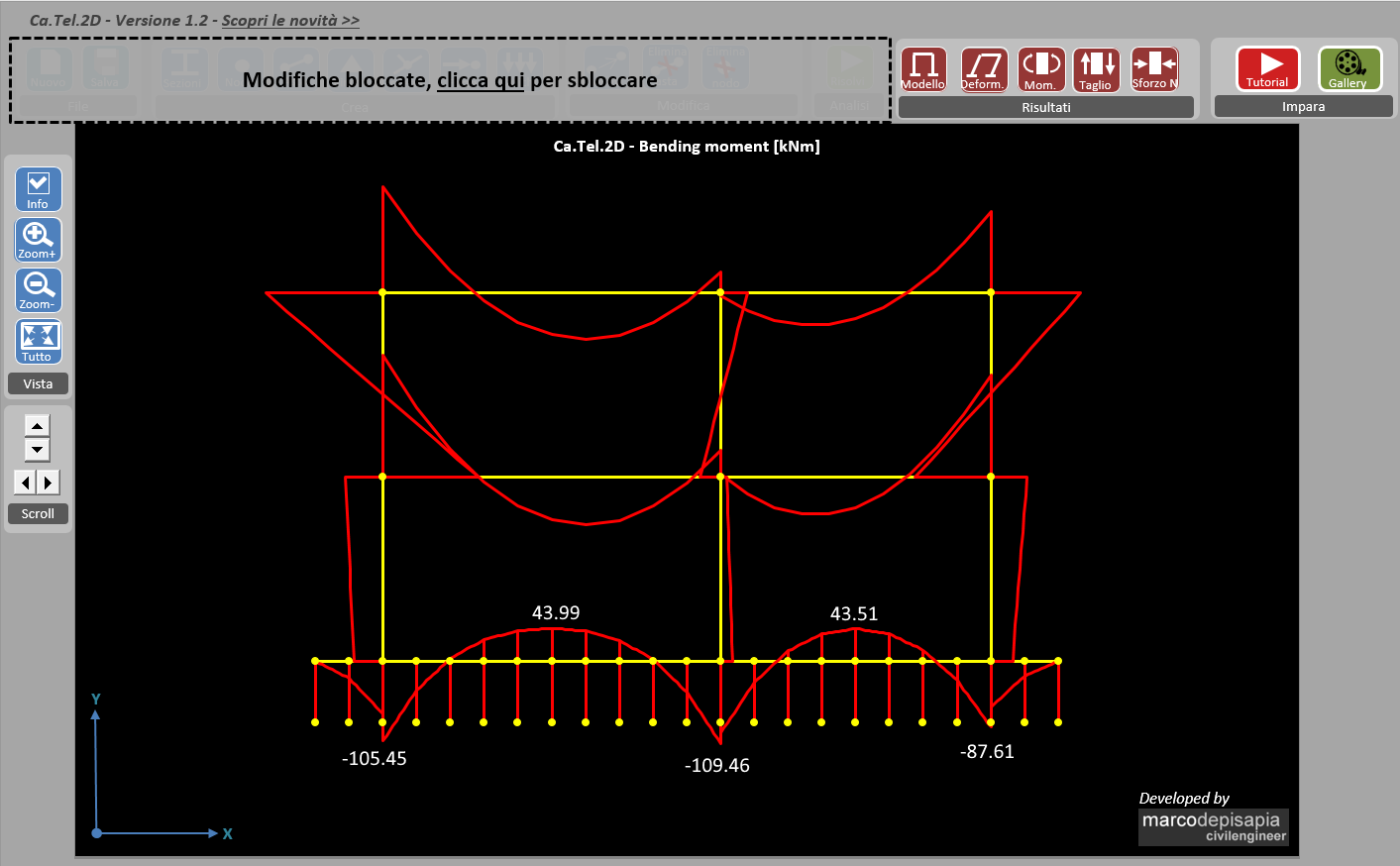
Come puoi vedere dall’immagine della deformata, l’eccessiva deformabilità della trave di fondazione non consente una distribuzione uniforme delle tensioni di compressione sul terreno.
Si avrà una concentrazione di sforzi in corrispondenza dei pilastri, mentre il resto del terreno al centro delle campate risentirà molto poco della presenza della sovrastruttura in termini di tensioni di compressione.
Ovviamente si tratta di una caso limite di esempio che mette in luce come una una fondazione non adeguatamente rigida non consenta di sfruttare appieno la capacità portante del terreno, in quanto i maggiori abbassamenti saranno concentrati in prossimità dei pilastri.
Secondo schema limite: trave di fondazione infinitamente rigida
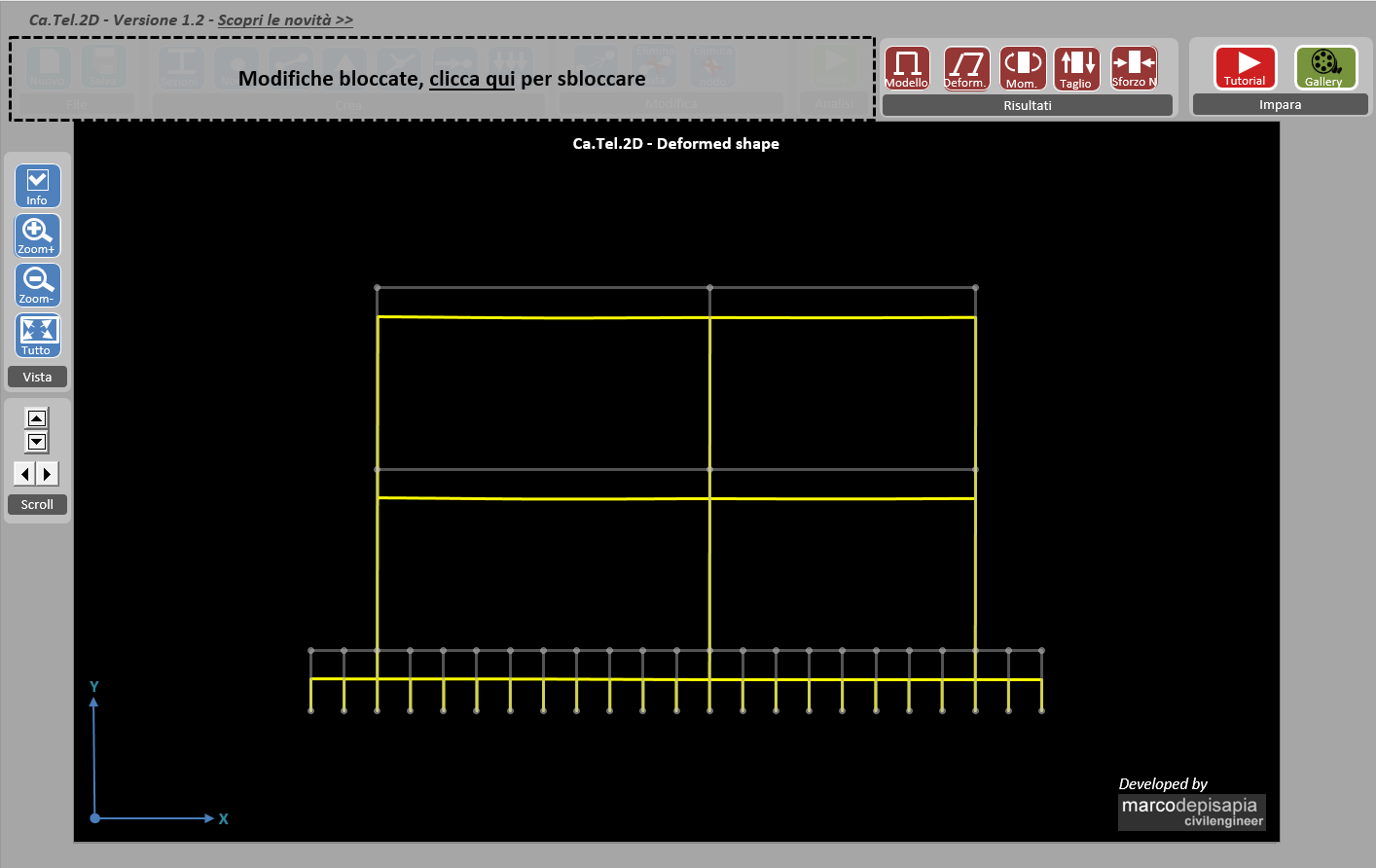
Nel secondo schema limite la trave di fondazione ha una sezione di rigidezza infinita. In Ca.Tel.2D ho assegnato alla trave una sezione con momento d’inerzia 1000 volte più grande rispetto al momento di inerzia di una sezione 40×100. Ti mostro sotto i risultati ottenuti in termini di spostamenti e sollecitazioni.
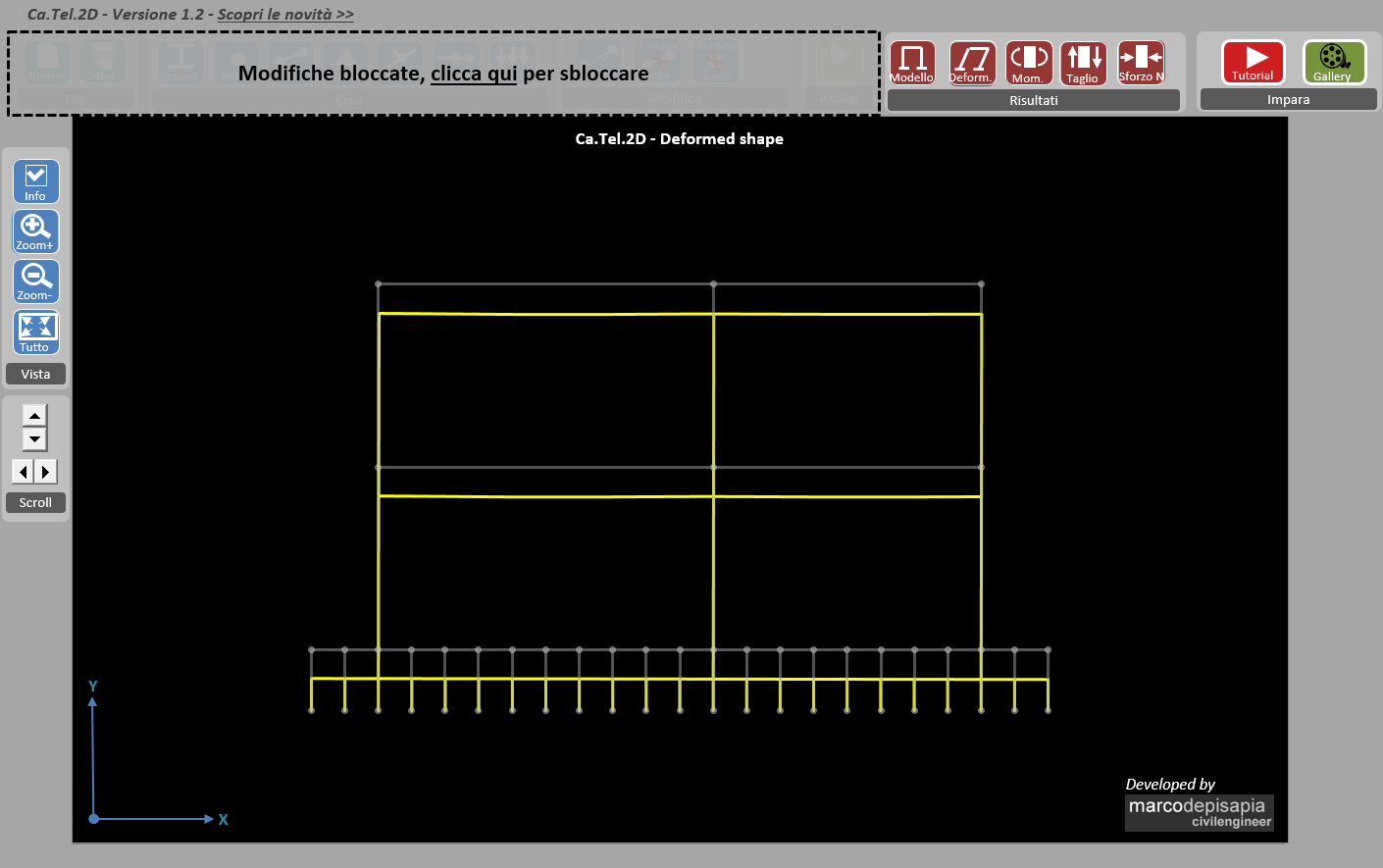
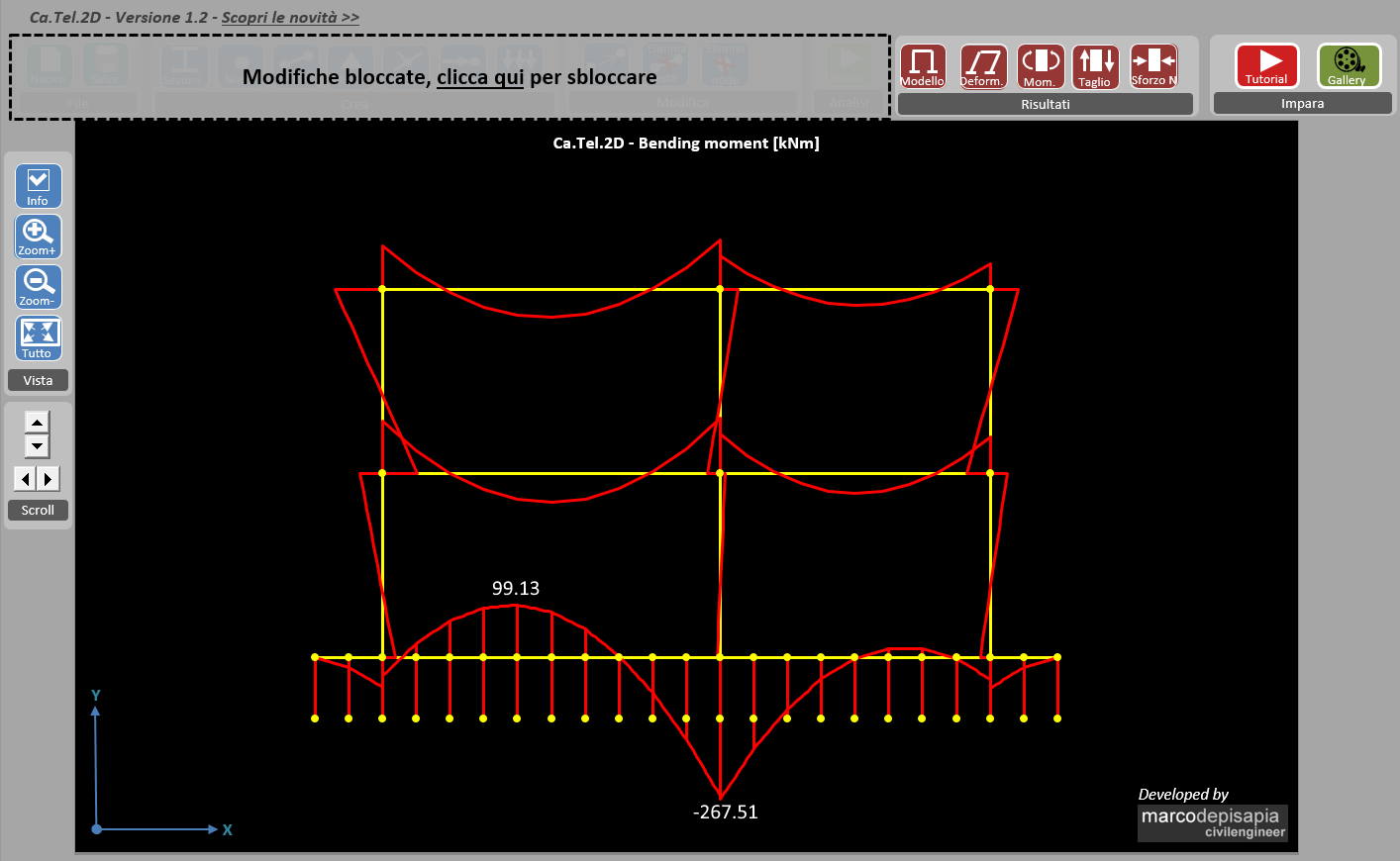
In questo caso la fondazione rigida trasla uniformemente verso il basso. L’abbassamento del terreno è uguale in ogni punto della fondazione e la tensione di compressione nel terreno è uniforme lungo l’asse della trave.
Le sollecitazioni flettenti nella trave di fondazione hanno un valore più grande rispetto al caso di fondazione con bassa rigidezza flessionale:
- primo schema limite – trave di fondazione con bassa rigidezza flessionale: momento massimo = 109.46 kNm;
- secondo schema limite – trave di fondazione infinitamente rigida: momento massimo = 267.51 kNm
Il momento sollecitante massimo aumenta, assumendo un valore pari a circa 2.5 volte il momento massimo della fondazione flessibile. La trave rigida comprime il terreno in maniera uniforme, facendo collaborare il terreno più distante dai pilastri.
Trave di fondazione su suolo alla Winkler: la realtà sta nel mezzo
I due casi limite appena visti mettono in evidenza l’importanza della rigidezza relativa fondazione/terreno.
Vediamo ora l’ultimo caso: una fondazione di rigidezza finita, corrispondente al caso di una sezione a T di altezza 100 cm, base 100 cm e spessore 40 cm.
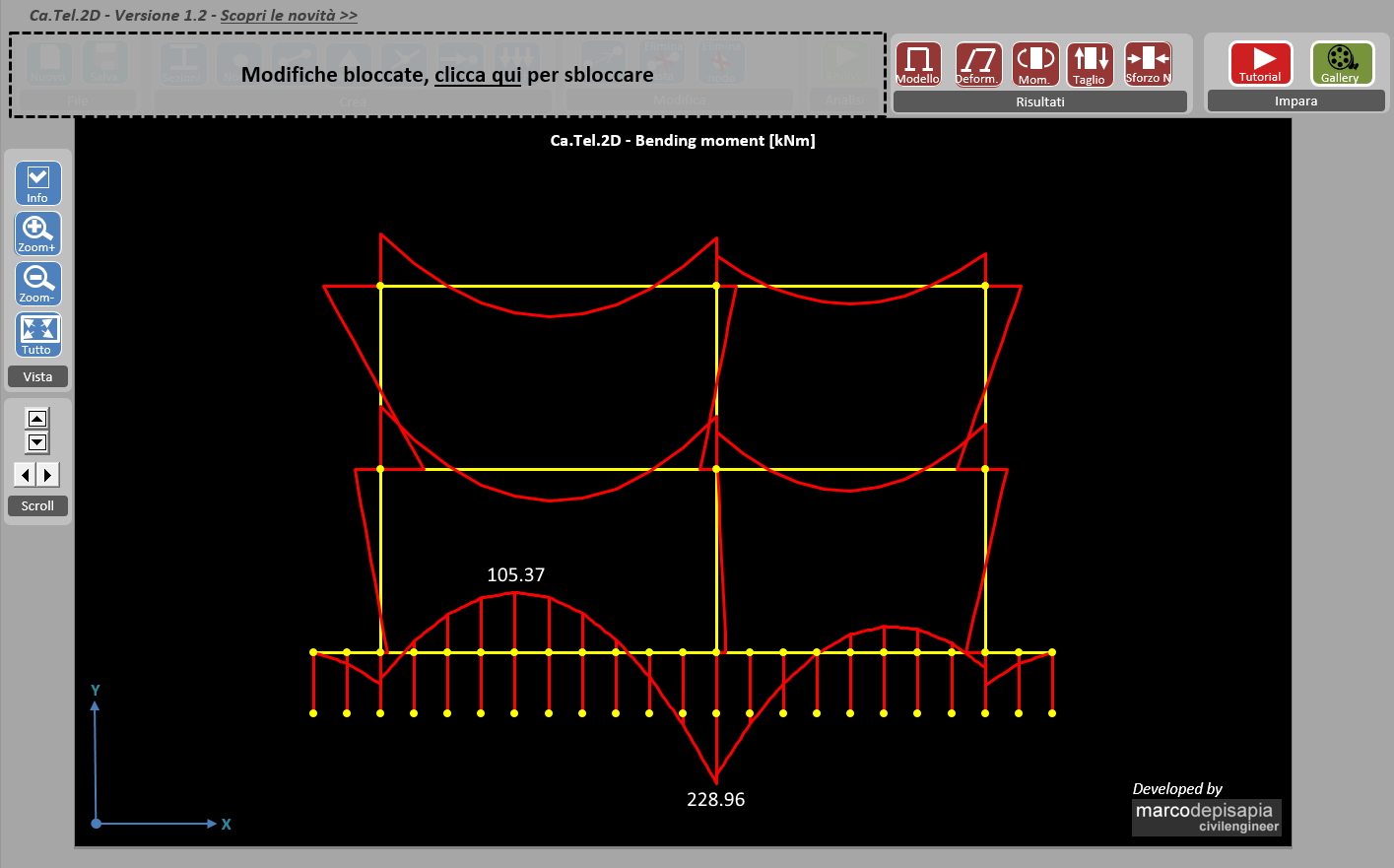
Come puoi vedere dalle immagini, i risultati in termini di spostamenti e sollecitazioni si avvicinano molto al caso di fondazione infinitamente rigida. Lo scostamento dei valori è davvero minimo.
- Momento massimo nella trave infinitamente rigida: 267.51 kNm;
- Momento massimo nella trave di rigidezza finita: 228.96 kNm.
Dai risultati ottenuti possiamo dedurre che in fase di predimensionamento delle strutture di fondazione sarà possibile utilizzare il modello di trave rigida per calcolare con buona approssimazione le sollecitazioni nella trave di fondazione.
La sensibilità del k di Winkler
In questo secondo esempio ti mostro come variano le sollecitazioni nella trave di fondazione al variare del k di Winkler, lasciando inalterata la sezione della fondazione. I due modelli analizzati sono caratterizzati dai seguenti valori della costante di sottofondo:
- k di Winkler pari a 3 kg/cm^3;
- k di Winkler pari a 0.3 kg/cm^3, dieci volte inferiore rispetto al caso precedente.
Di quanto pensi varieranno le sollecitazioni nella trave di fondazione nei due casi? Te lo mostro subito.

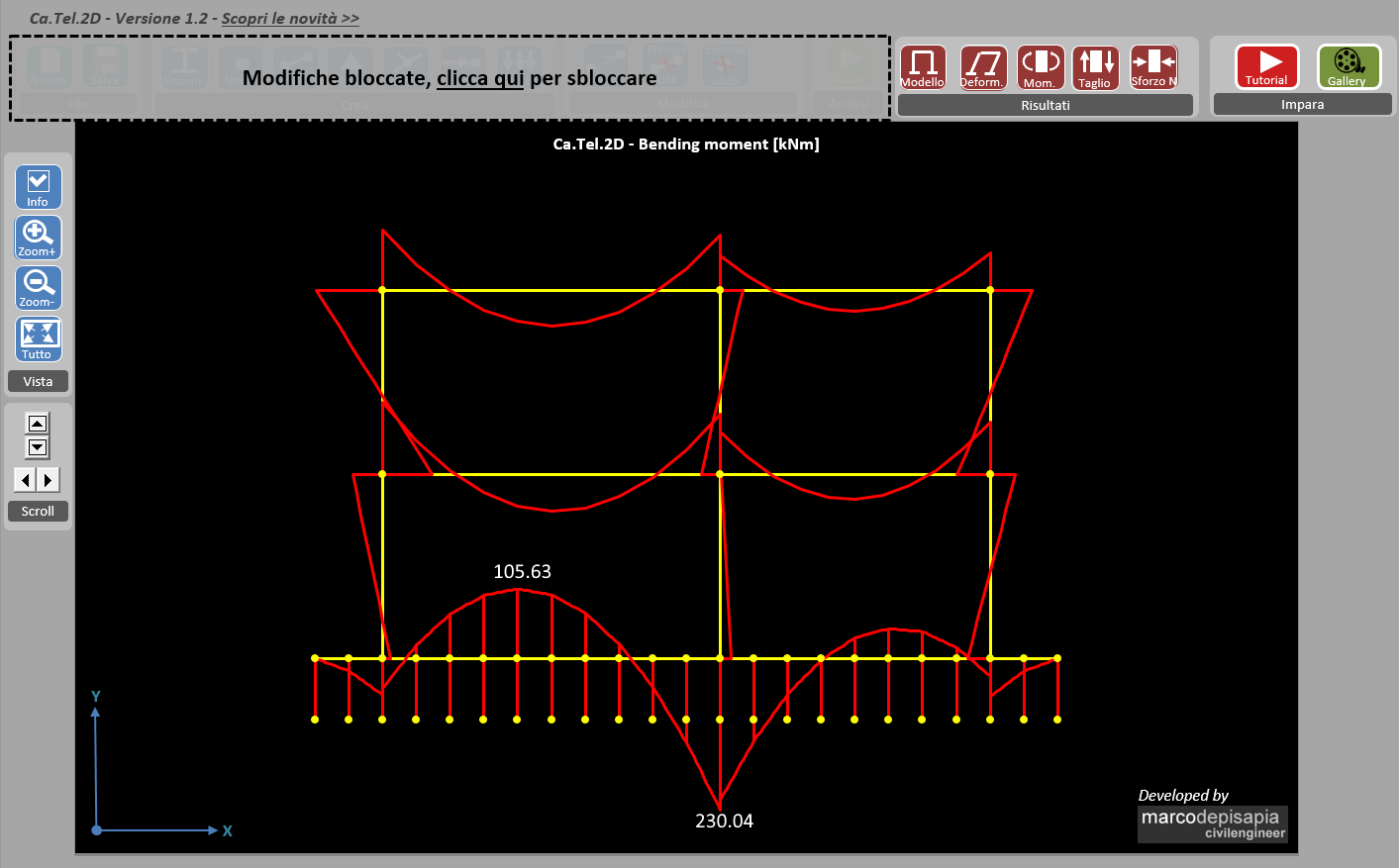
- k = 3 kg/cm^3; momento massimo = 228.96 kNm;
- k = 0.3 kg/cm^3: momento massimo = 230.04 kNm.
Le sollecitazioni nella trave di fondazione risentono molto poco della variabilità del k di Winkler. Si ottengono valori del momento massimo che sono praticamente coincidenti. Pertanto se la costante di sottofondo del terreno viene stimata in modo approssimato, non si commetteranno grossi errori nella valutazione delle sollecitazioni.
Variabilità del k di Winkler: il caso notevole del riempimento di uno scavo
Diverso è il caso in cui il k di Winkler varia lungo l’asse della trave, assumendo due valori differenti. In questo caso le sollecitazioni nella trave di fondazione ne risentono sensibilmente.
La variabilità del k di Winkler in direzione orizzontale può essere causata dal riempimento di uno scavo localizzato di dimensioni inferiori alla lunghezza della fondazione, utilizzando materiale di riporto senza eseguire un adeguato compattamento. In tal caso il suolo di fondazione avrà due differenti costanti di sottofondo.
Nell’esempio seguente il k di Winkler è pari a 3 kg/cm^3. In corrispondenza della porzione di terreno sotto il pilastro centrale assume un valore ridotto di 0.3 kg/cm^3.
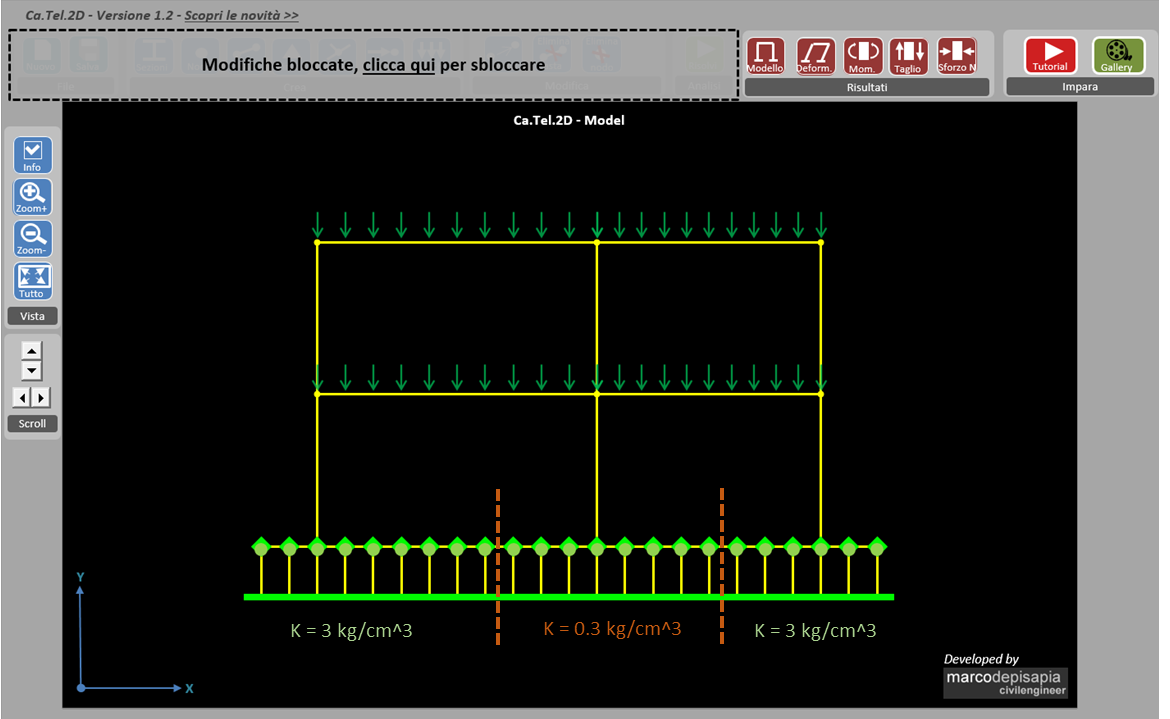
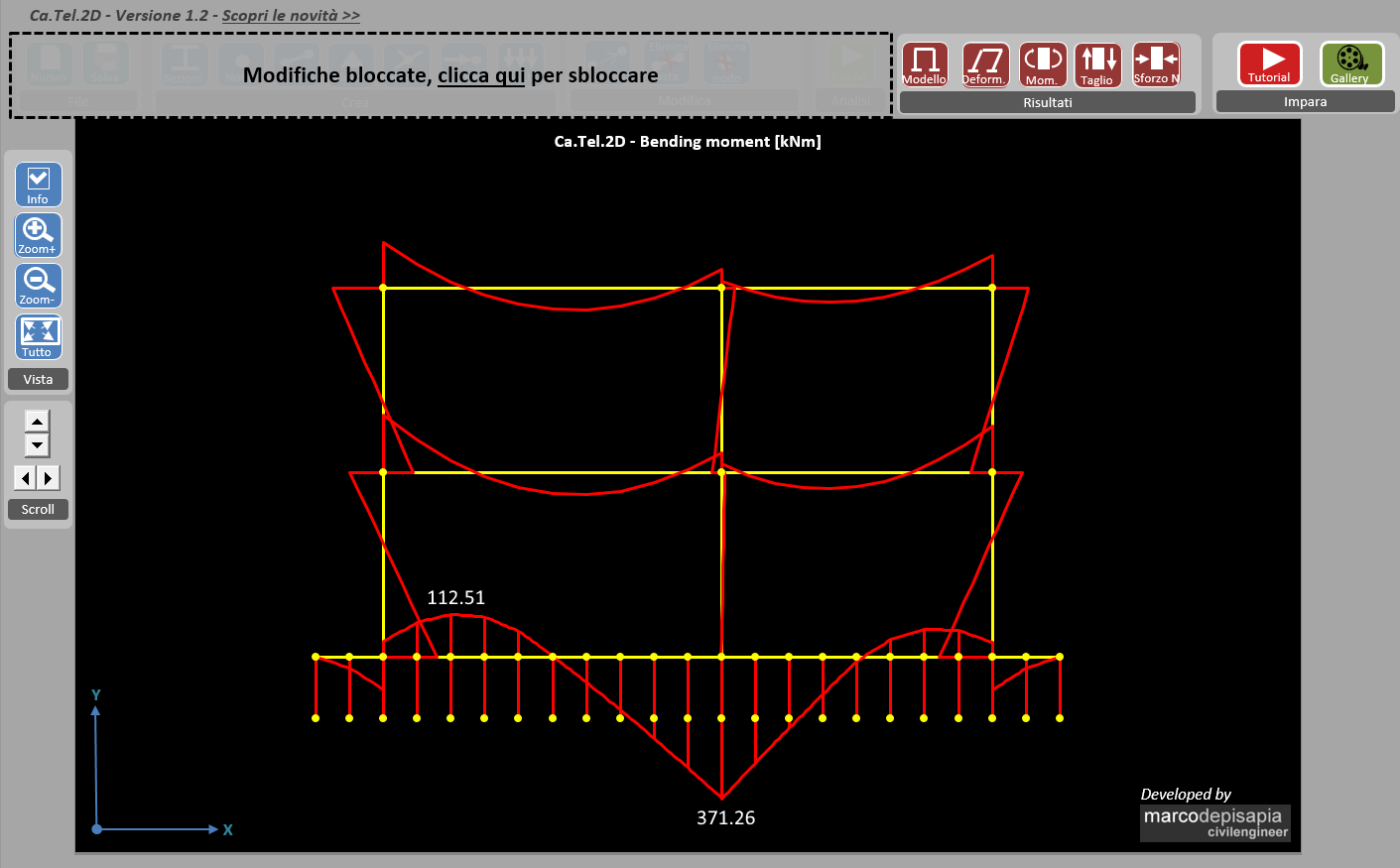
In questo caso le sollecitazioni della trave assumono un andamento del tutto differente rispetto al caso di suolo omogeneo con rigidezza di Winkler uniforme. Il valore massimo del momento aumenta considerevolmente, passando da un valore di circa 230 kNm ad un valore di 371 kNm (incremento di ben il 60%).
Gli effetti del suolo alla Winkler sul periodo di vibrazione delle costruzioni
Se modelli la struttura con trave di fondazione su suolo alla Winkler, aumenteranno i periodi propri di vibrazione rispetto al caso di struttura con vincoli di incastro alla base. Di conseguenza si avrà una variazione dell’accelerazione spettrale ai fini del calcolo dell’azione sismica.
Al diminuire della rigidezza traslante, aumentano i periodi di vibrazione (ottenuti mediante analisi modale). Per rendertene conto puoi osservare la formula del periodo di vibrazione di un oscillatore semplice:
T = 2 π √( M / K )
- M = massa concentrata dell’oscillatore semplice;
- K = rigidezza traslante dell’oscillatore semplice;
- T = periodo di vibrazione.
Ti riporto un esempio che mostra la diminuzione di rigidezza traslante passando da un telaio a base fissa ad un telaio con trave di fondazione su suolo alla Winkler. I due telai mostrati di seguito sono caricati da una forza orizzontale pari a 100 kN applicata nel nodo di sommità.
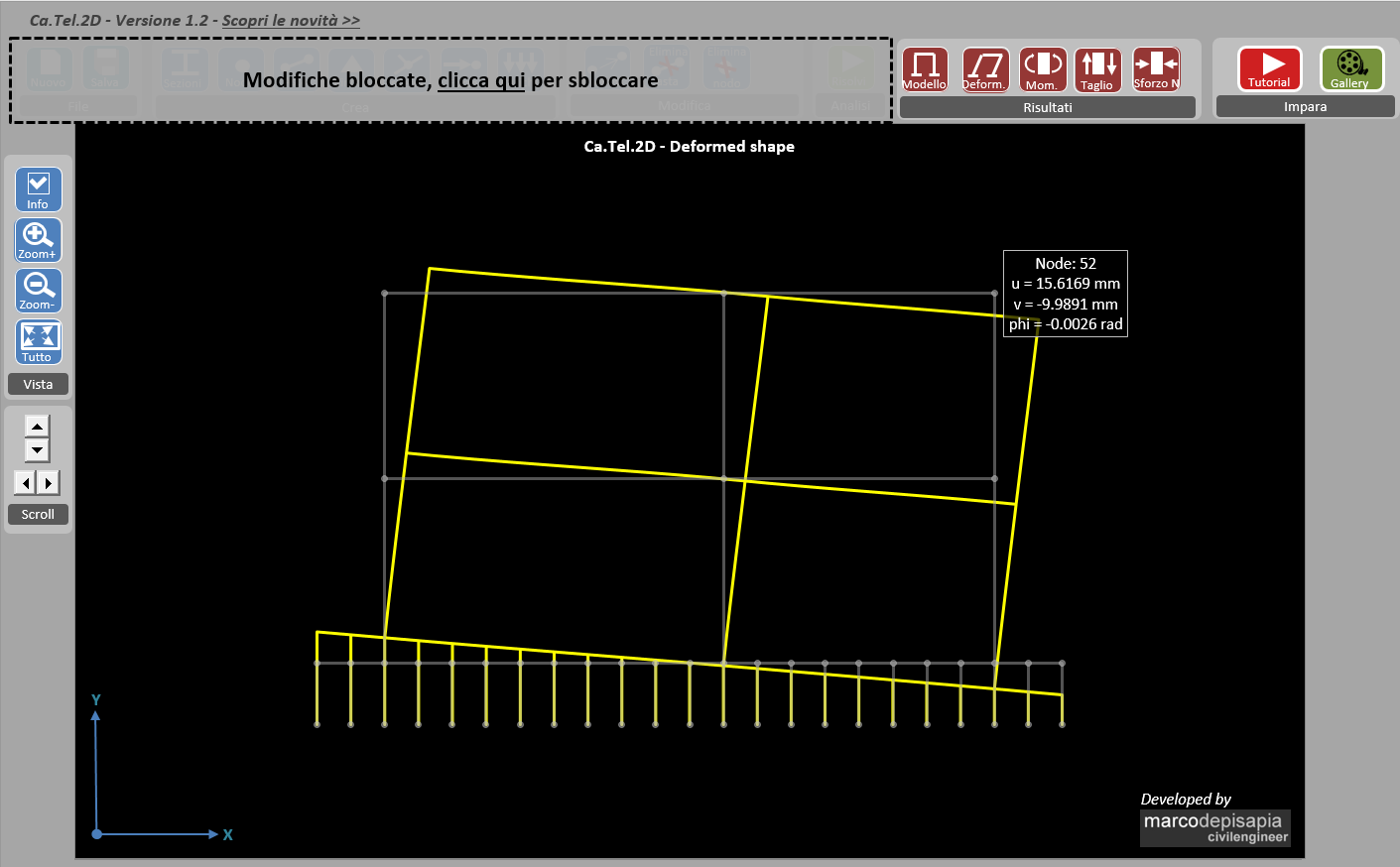
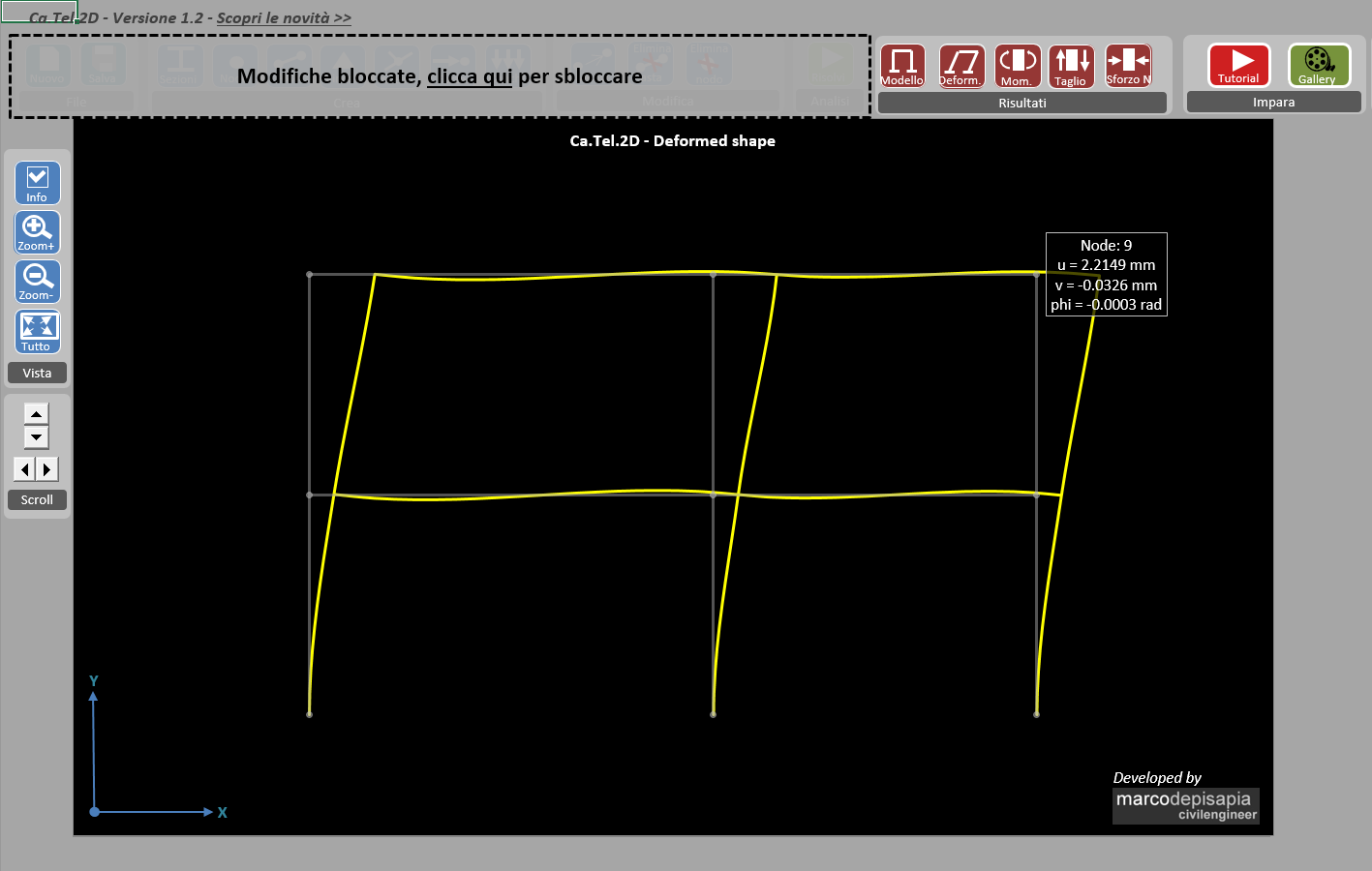
Il telaio con trave di fondazione su suolo alla Winkler presenta uno spostamento orizzontale del nodo di sommità più grande di quello a base fissa (15.62 mm contro 2.21 mm), di conseguenza avrà una rigidezza traslante più bassa.
Ti consiglio di modellare la fondazione su suolo alla Winkler solo se la stima del k di Winkler può essere ritenuta rappresentativa della reale rigidezza del terreno; in caso contrario, ai fini dell’analisi sismica della struttura, è preferibile modellare la struttura con incastri alla base.
Conclusioni
Siamo arrivati alla fine di questo lungo post. Ecco cosa devi ricordare quando progetti e verifichi una trave di fondazione:
- per poter analizzare un modello completo di trave di fondazione su suolo alla Winkler, dovrai controllare che il tagliante alla base e il carico verticale globale sia almeno pari al 70% dei corrispondenti valori ottenuti dal medesimo modello con incastri alla base;
- le sollecitazioni ottenute per trave di fondazione infinitamente rigida sono quasi coincidenti con le sollecitazioni per trave di fondazione con rigidezza finita. In fase di progetto quindi puoi calcolare le sollecitazioni utilizzando il modello di trave di fondazione infinitamente rigida;
- le sollecitazioni nella trave di fondazione risentono poco della variabilità del k di Winkler se questo resta costante lungo l’asse della trave;
- le sollecitazioni nella trave di fondazione possono variare di molto se il k di Winkler varia lungo l’asse della trave in corrispondenza di una o più campate (caso di scavi localizzati riempiti in seguito con materiali di riporto).
Per oggi è tutto. Se hai trovato utili le informazioni contenute in quest’articolo, puoi suggerirle ad un tuo collega su Linkedin o ad un tuo amico su Facebook cliccando sui tasti di condivisione che trovi in fondo alla pagina.
Ci rileggiamo al prossimo articolo.
Marco
Risorsa consigliata: Plate Design, l’app per il calcolo di platee di fondazione su suolo alla Winkler

Per eseguire l’analisi, il progetto e la verifica di fondazioni superficiali a platea puoi utilizzare Plate Design, l’app del blog per la risoluzione del problema statico di una piastra su suolo elastico alla Winkler.
Plate Design ti consente di analizzare le sollecitazioni della piastra di fondazione, progettare e verificare l’armatura della platea, eseguire la verifica geotecnica per carico limite e scorrimento. Puoi eseguire il download dell’app cliccando sul bottone qui sotto.
Aggiornato il 8/6/2020. Pubblicato il 4/9/2017.

