Nuovo tutorial in formato video sull’utilizzo di Ca.Tel.2D, l’applicazione del blog per l’analisi di schemi strutturali piani. Nel video-tutorial di oggi ti mostro come modellare una trave di fondazione su suolo alla Winkler per poter calcolare le sollecitazioni e gli spostamenti. Ti mostrerò come creare i vincoli elastici alla base della trave (molle di Winkler) grazie a dei pendoli e quali proprietà assegnare alla sezione di questi elementi.
Alla fine dell’articolo potrai scaricare una nuova risorsa riservata agli iscritti. Ti permetterà di calcolare in automatico il modulo elastico della sezione del pendolo per poter riprodurre il k di Winkler necessario.
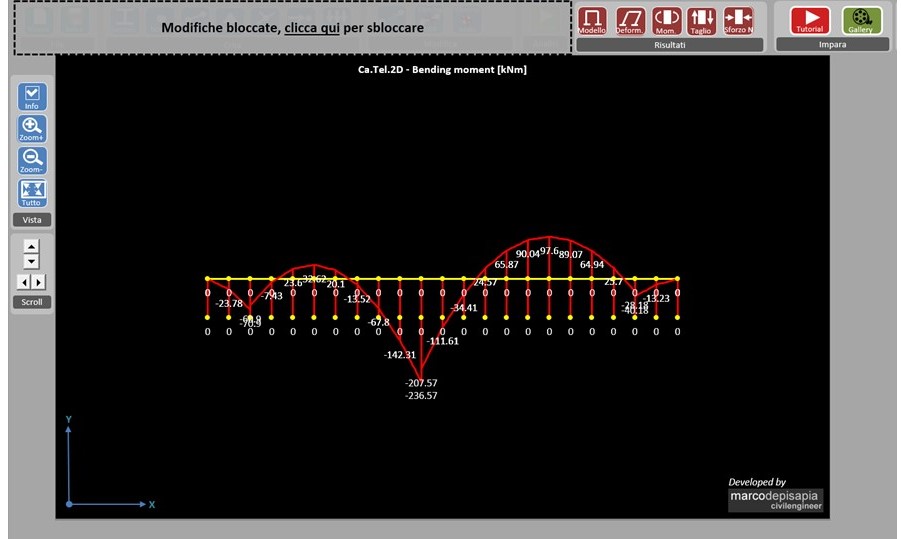
Guarda il video-tutorial sulla trave di fondazione
ERRATA CORRIGE: il valore del modulo elastico mostrato nel video deve essere pari a 166,7 N/mmq invece di 16,7 N/mmq.
Come creare il vincolo di suolo alla Winkler
Ti è piaciuto il video? Come hai potuto vedere per creare il vincolo di suolo alla Winkler bisogna assegnare le giuste proprietà alla sezione dei pendoli alla base della trave. Ti riassumo le proprietà che il pendolo deve avere per riprodurre il vincolo alla Winkler:
- lunghezza del pendolo: 1 metro;
- vincoli: incastro alla base del pendolo – cerniera interna all’estremità a contatto con la trave;
- sezione del pendolo: 30 cm x 30 cm;
- modulo elastico: da calcolare in funzione della base della fondazione, della lunghezza dei segmenti in cui è stata divisa la trave (nell’esempio 0.5 metri) e del k di Winkler del terreno. La risorsa che potrai scaricare tra poco ti permetterà di calcolarlo in automatico;
- vincolo esterno dei nodi della trave di fondazione: traslazioni lungo X bloccate.
Scarica la risorsa
Per renderti più semplice calcolare il modulo elastico da assegnare alla sezione, ho creato una semplice risorsa in cui potrai inserire i dati di input e ottenere in automatico il modulo elastico da assegnare alla sezione dei pendoli di base. I dati che dovrai inserire sono i seguenti:
- base della fondazione;
- lunghezza dei segmenti in cui hai suddiviso la fondazione (0.5 metri nell’esempio);
- k di Winkler.
La risorsa è riservata agli iscritti al blog. Se non sei ancora iscritto puoi rimediare subito compilando i campi sottostanti. Riceverai all’istante un’email con il link per eseguire il download.
Conclusioni
Hai trovato utile il nuovo video-tutorial di oggi? Se ti è piaciuto puoi suggerirlo ai tuoi amici sul tuo social preferito o ai tuoi colleghi su Linkedin cliccando sui tasti di condivisione che trovi in fondo alla pagina.
Al prossimo articolo.
Marco
Articoli correlati
- Come progettare una fondazione: rigidezza sezione e k di Winkler
- Interazione fondazione-terreno: 3 metodi di calcolo di una platea
